文系のあなた!文系だからと言って理系の数学的な分析・思考力は学ばなくていいと思ってないですか?データ解析能力が足りないと感じている社会人は多いし、それどころかデータ解析を見ないフリする社会人はとっても多い。実際には、大半の会話についていくための知識は、そんなに多くないんです。本っ当に最低限の知識を、本っ当にわかりやすくまとめたので、文系のあなた、是非見てください!
- 社会人生活においてツブシがきく数学的知識が知りたい学生・社会人
- 文系出身で数学を諦めてきた社会人
- 理系出身だけど実は数学的知識をおさらいしておきたい社会人
- 中学生でもたぶん大丈夫
ども!パワハラ環境を自力で脱出した脱獄リーマンこと高岡陽也と申します!
私は文系だからと、数学的な知識を見ないふりする人が本当に多くてもったいない。ちょっと勉強するだけでも大きく知見が広がるんだ!ぜひ一緒に学んでいきましょう!
理系でなくても数学的知識があった方が強い!

よし!予想通り顧客は僕が提案したサービスを評価してくれたぞ!

きゃ!私が提案した商品、発売したのに売上ゼロ!?
なぜか理系の人が考えた提案の方が正解率が高い、そんな事を思った事はないかな?それは、センスではなく、数学的知識を基礎としたデータサイエンスに関する知識があるかないかが原因であることが多い。感覚的には捉えきれない事象を正しく捉えることができるようになるんだ!もちろん、理系である必要は全くない。最低限の数学知識ならば誰でも身につけられるし、論理的思考力があれば、データサイエンスの基礎を身につけて新しい世界が開けるよ。
全4回に分けて、データ分析の考え方を伝授したいと思っているよ。もう、めっちゃ簡単にね。文系の言語能力・表現能力・柔軟性に理系の必携知識を合わせれば鬼に金棒だ!さあ「ザ・文系」のレッテルを脱ぎ捨てよう!自信と選択肢が広がるよ!
第1回は、全体像の理解だ!どんなことを勉強するべきなのか、これを見るだけでさっと掴めるよ!
データ・数学の基礎知識を押さえる
ここは第2回で詳しく説明する予定だけど、パンに例えて概要は説明しておくよ!とは言え、結構ここだけでわかるように書ききってしまった。
数学知識:ばらつき(安定してるパン屋と不安定なパン屋)
同じ平均値のデータも、中身を除けば千差万別。それがわかる一つの指標が「ばらつき」です。ある店舗の売上データを例に考えてみよう。この「ばらつき」を正しく理解することが進んだ分析の第一歩だ!
- 平均売上高が1日あたり10,000円の店舗が2店舗ある
- しかし、実態を見ると全く違っている
- 店舗A:毎日10,000円の売上
- 店舗B:曜日によって全然違う売上
- この時、店舗Bは店舗Aよりも「ばらつきが大きい」 と言う。
⇛どちらの店舗にも毎日同じ人数の店員を配置すると、
店舗Bでは売れない時は店員の過剰、売れる時は店員の不足が生じるよね。
 毎日、普通に売れる店舗A
毎日、普通に売れる店舗A  時々すごい店舗B
時々すごい店舗B
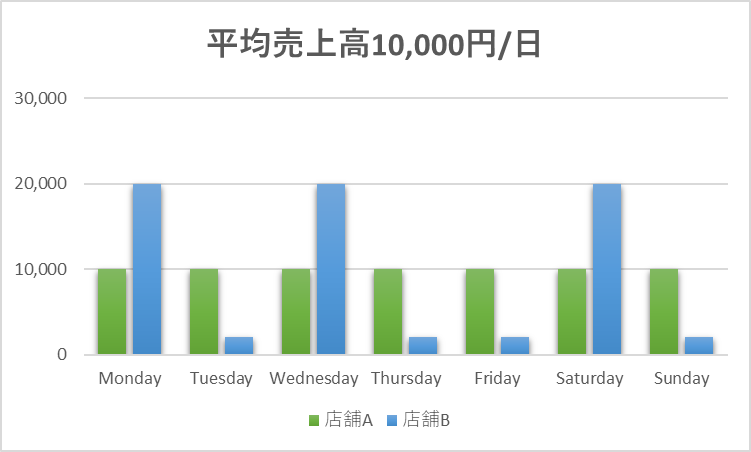
店舗B(青)は、店舗A(緑)よりも売上高のばらつきが大きい
この「ばらつき」を定量的に表す指標に標準偏差がある。これは、全データの中でのズレの度合いを表しています。よくある正規分布という範囲に従うと仮定した場合、平均10,000円日、標準偏差500円の場合、9,500円日から10,500円日の間に売上が収まる確率が68%、9,000円日から11,000日円に収まる確率が95%だとわかるんだ。どんくらいバラついているかイメージがつくってこと。詳しくは第2回で。
数学知識:分布(安くたくさん売るパン屋とお高く限定販売するパン屋)
次に「分布」の理解です。売上データを棒グラフに表すと、例えばある金額付近に集中する傾向がわかります。このデータの分布をつかむことも重要です。
- データを棒グラフなどで可視化すると、金額別に売上枚数の分布が分かります。
- ある金額帯に売上が集中するなど、データの集まり方を分布と呼びます。
- 分布から売上の多い金額帯が一目で分かるので重要です。
 お安いパンを大量に売る店舗C
お安いパンを大量に売る店舗C  お高いパンしか売らない店舗D
お高いパンしか売らない店舗D
数学知識:代表値(平均値、中央値、最頻値)
代表値として「平均値」「中央値」「最頻値」というものがある。
「市民感覚は、年収の平均値より年収の中央値の方が近い」などとよく言われるけど、その中央値とは何か、とかそのあたりを説明するよ。目的に応じて適切な代表値を使い分けられるようになろう。
ここでは、安いパンから高いパンを順番に並べてみよう。
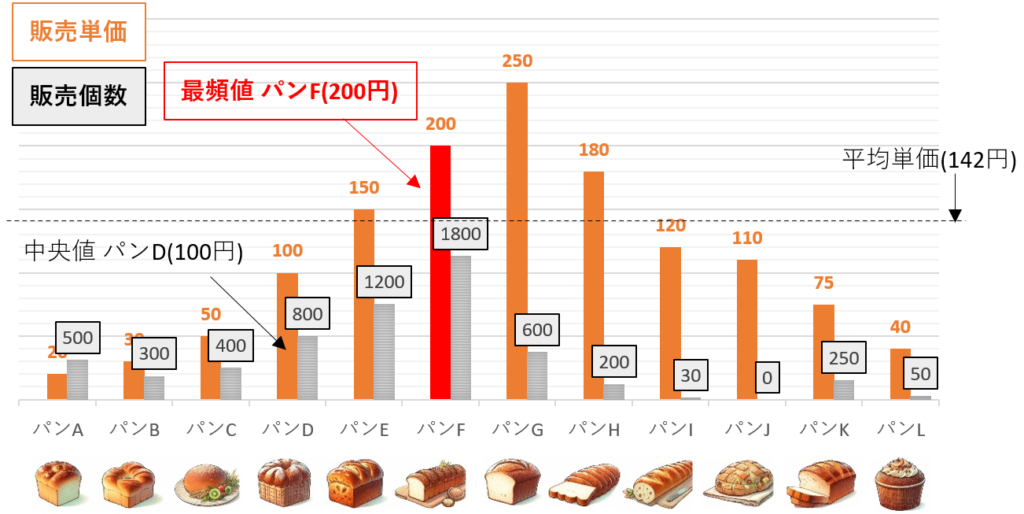
で、パンの販売単価に関する値を見てみよう。パンAからパンLまで、12種類を並べてみた。
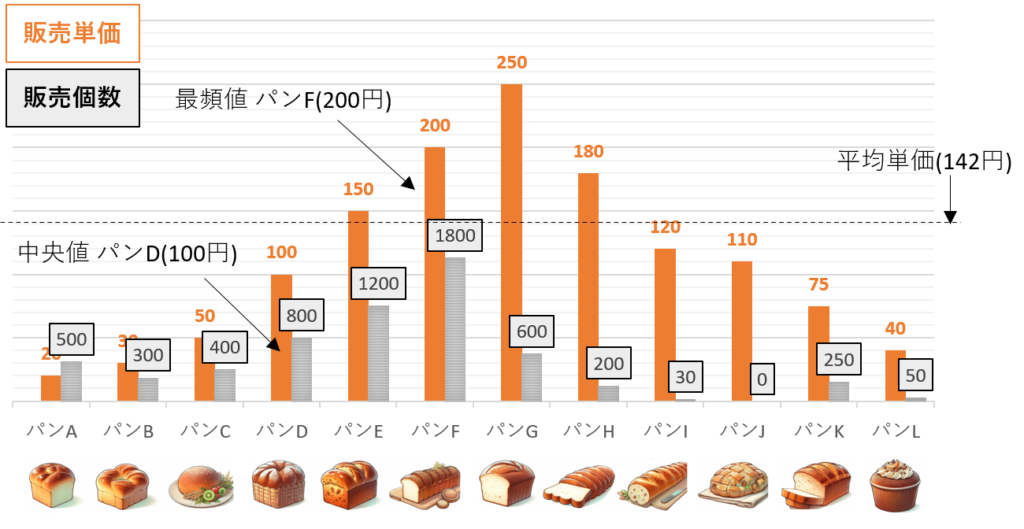
平均値(あの店のパンはだいたいいくら その1)
ほとんど皆知っているとは思うけど、全データの合計をデータ数で割った値で、「このデータの中で典型的な値とは何か」を表すんだ。今回の場合は、合計の販売金額を販売個数で割ったものが「平均値」だ。パン1コあたり平均いくらなのか。下記の例では 142円 だ。
社会人としては、単純平均・加重平均の違いくらいは必ず抑えておきたいけど、これはまた次の機会で。今回は「加重平均」で考えているよ。
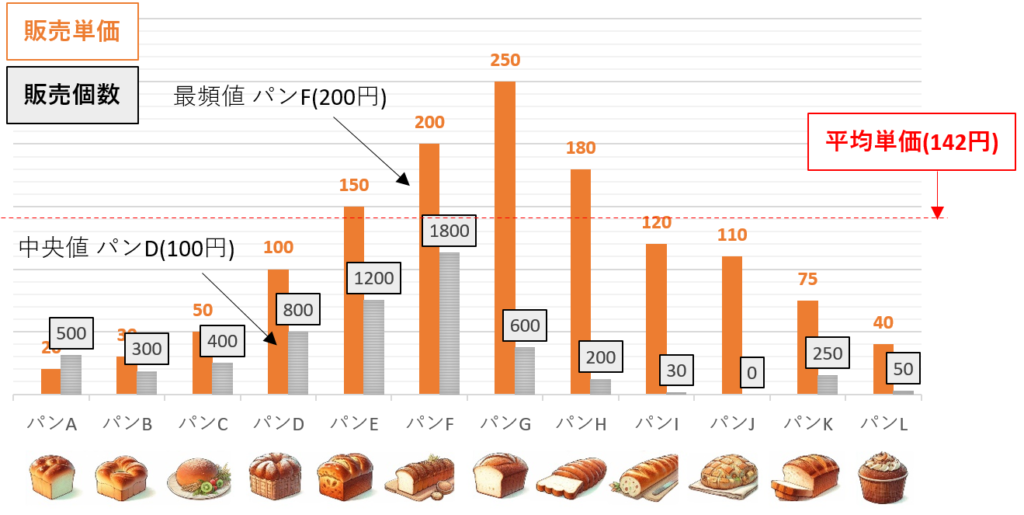
中央値(あの店のパンはだいたいいくら その2)
真ん中にある値です。もう物理的にそのまんま、データの真ん中にある値 を表すよ。「前へならえ!」をして真ん中にいる人。真ん中のデータが「中央値」だ。安いパンから高いパンまで順番に並べて、真ん中に売れたパンがいくらなのか。
このグラフだと、合計6,000コくらいパンが売れていて、およそ3,000コ目は 100円のパンD だ!(実際は 6,130コ中の3,065コ目の事だよ。)
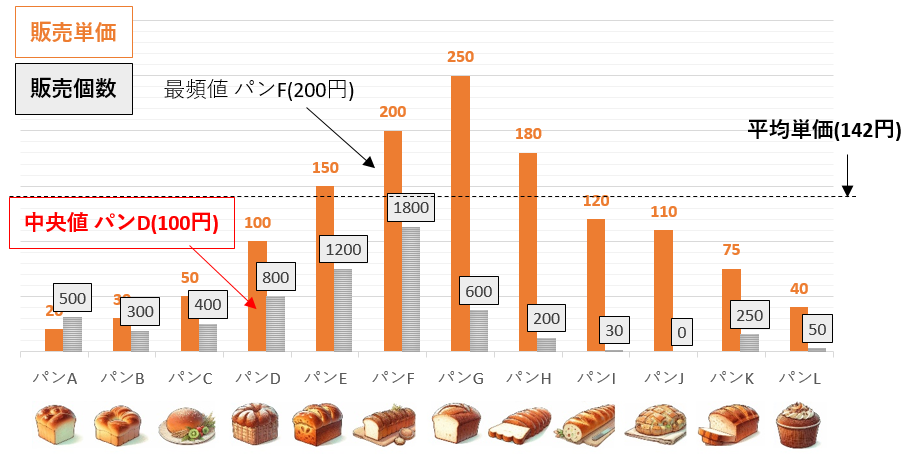
最頻値(あの店で一番売れているパンはいくら)
最も出現する値で、どの値が集中して出現しているかを表すよ。最も頻繁に出現する値が「最頻値」だ。最も売れたパンがいくらかだよ。今回の例では、パンFが1,800コと一番売れているから、最頻値はパンFの200円だ。
数学知識:相関関係(世の中でアイスが売れまくったら、あのパンは・・・)

2つのデータにどの程度関連があるかを表す値だよ。相関係数、と言ったら吐きそうになるかもしれないが本当に簡単だから見てくれい。
例えば世の中でアイスがめちゃめちゃ売れると、パンの売れいきがこうなるとしよう。
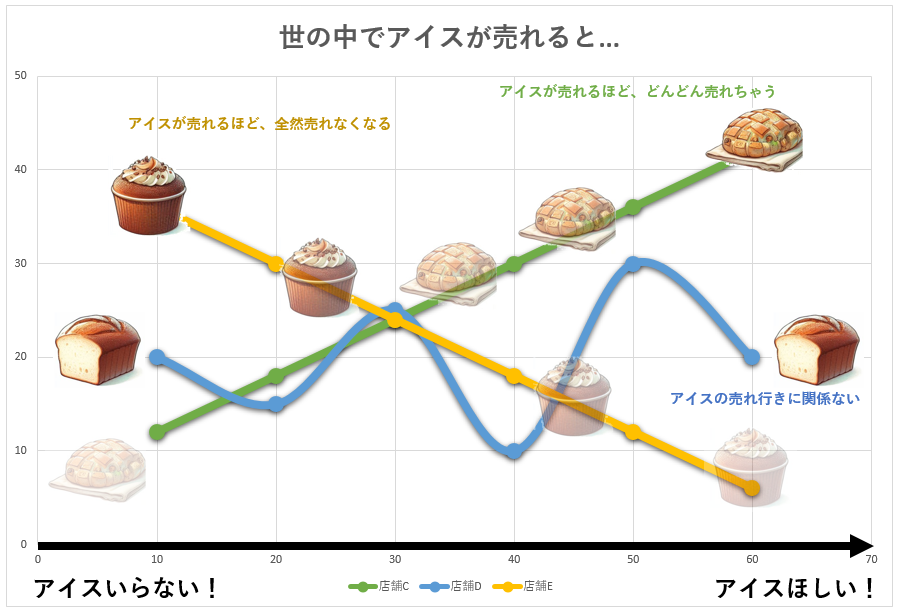
- めちゃめちゃ売れるパン
- いつもと変わらないパン
- めちゃめちゃ売れなくなるパン
があるね。世の中のアイスと、それぞれのパンの売上には何か説明ができそうだねぇ。この関連の度合いを感覚的ではなくて、定量的に表したものが相関係数だよ。相関係数は、小数点以下を交えて+1~-1で表されるんだ。
正の相関(世の中でアイスが売れると、めちゃめちゃ売れるパン)

この場合、アイスとパンの売れ行きには「正の相関がある」というんだ。
この正の相関、相関が強ければ強いほど、相関係数は+1に近い値をとるんだ。
アイスが売れたら良い意味でやべえパン、だね。
相関係数が、+0.5と+0.9では、後者の方がアイスの売れ行きに相関があって良い意味でやべぇっす。
無相関(世の中でアイスが売れても、関係ないパン)
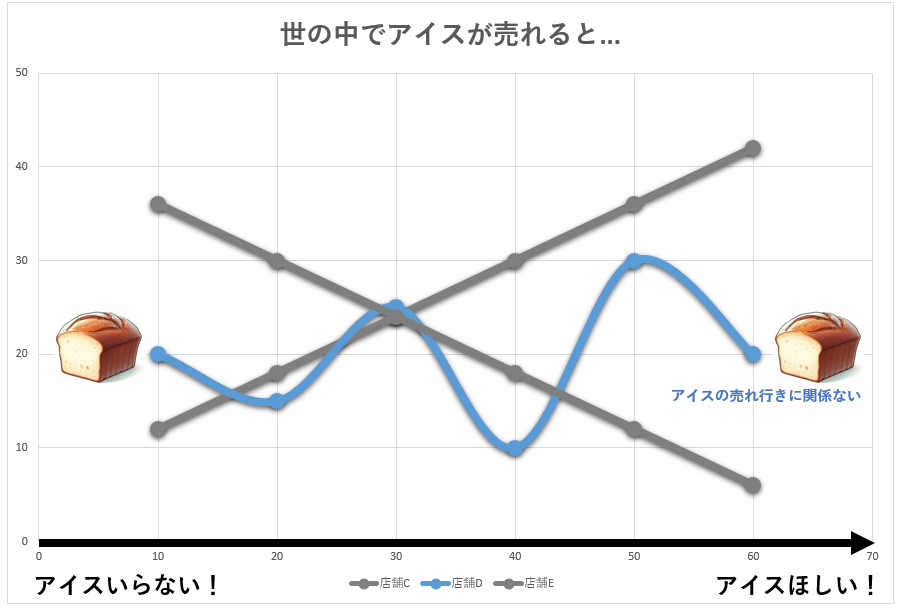
こちらはアイスとパンの売れ行きに相関がないケースだよ。アイスの売れ行きが好調でも不調でも、パンの売上に影響がないよ。相関係数は0、つまり無相関を示します。
この相関が弱ければ弱いほど、相関係数は 0 に近い値をとるんだ。
アイスが売れても関係ねぇパン、だね。
相関係数が、+0.2と+0.1では、後者の方がアイスの売れ行きに相関せず関係ねぇっす。
負の相関(世の中でアイスが売れると、めちゃめちゃ売れなくなるパン)

このケースではアイスとパンの間に「負の相関がある」と言うよ。アイスが売れる分、逆にパンの売上が減少してしまうんだ。相関係数は-1に近い負の値になるよ。
この負の相関、相関が強ければ強いほど、相関係数は-1に近い値をとる。
アイスが売れたら逆にやべえパン、だね。
相関係数が、-0.6と-0.8では、後者の方がアイスの売れ行きに相関があって逆にやべぇっす。
以上の例で、相関係数がデータの関連の強さを定量的に表す指標であることがわかったと思う!
考え方の基礎を学ぶ
ここは第3回で詳しく説明する予定だけど、パンに例えて概要は説明しておくよ!
数学知識:場合の数と確率(あのパンがもらえる確率)
「場合の数と確率」は論理的思考力を鍛える上で欠かせない。次のリスクと期待値にもつながるよ。
さまざまな事象の発生パターンを洗い出し、起こりうるケースの数を算出することがポイントだよ。
パン屋で販売しているパンの種類を考えてみよう。
例えばカップケーキ、食パン、クロワッサン、メロンパンの4種類があるとしましょうか。




ここで、来店したお客様に抽選でランダムに1つのパンをプレゼントすることを考えよう。 お客様が選ぶパンの種類は、まんま4通りがあるね。お客さんの意志に関係なくランダムに選ぶわけだから、これらはそれぞれ等しい起こりうる可能性を持っている。
なので、各々の場合(各パンを選ぶ場合)の確率は
1/4 = 0.25 = 25%
となります。
これを少し応用して、パンを2つプレゼントする場合を考えてみよう。
パンの重複を「あり」とする場合(同じパンが2回当たったりするときの確率)
パンの組み合わせは16通り存在して、特定の組み合わせが当たる確率は当たる順番も考慮すると
1/4 ✕ 1/4 = 1/16 = 0.0625 = 6.25%
となる。

 =6.25%
=6.25%
しかしカップケーキと食パンが当たる場合、どちらが先に当たろうが組み合わせに違いは起こらない。従って当たる順番を考慮しない場合は
1/4 ✕ 1/4 ✕ 2 = 1/8 = 0.1250 = 12.50%
となる。

 =6.25%
=6.25% 
 =6.25%
=6.25%
パンの重複を「なし」とする場合(同じパンが2回当たったりはしないときの確率)
パンの組み合わせは12通り存在して、特定の組み合わせが当たる確率は、当たる順番も考慮すると
1/4 ✕ 1/3(最初に当たったパンは当たらないから3種類しかない)
1/4 ✕ 1/3 = 1/12 ≒ 0.0833 = 8.33%
となる。
しかしカップケーキと食パンがあたる場合、どちらが先に当たろうが組み合わせに違いは起こらない。従って当たる順番を考慮しない場合は
1/4 ✕ 1/3 ✕ 2 = 1/6 ≒ 0.1678 = 16.78%
となる。

 =8.33%
=8.33% 
 =8.33%
=8.33%
数学知識:指数関数(SNSでめっちゃバズったパン)
 「う、美味そうな食パンを見つけたぞぉ」
「う、美味そうな食パンを見つけたぞぉ」 「あの食パンを出せー!」
「あの食パンを出せー!」
指数関数と対数関数は文系でも学んでおきたい関数だよ。普通に会話で使うし使われる。計算方法はExcelを頼ればなんとかなる。
2つの数値の特徴を理解して、これは指数関数だ、これは対数関数だ!とわかれば取っ掛かりはOK!
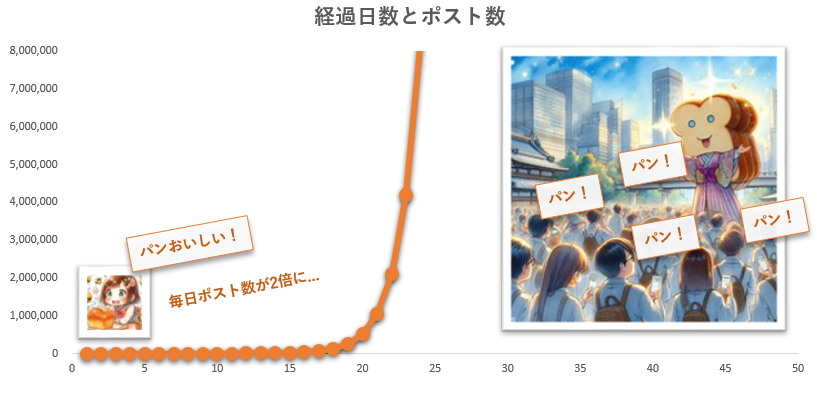
パンとSNSを説明に使おう。とあるパンが初めて店頭に並ぶと最初はゆっくりとしか売れなかった。でも、SNSなどで「このパン美味しい!」という口コミが拡散していくにつれ、売上が急激に伸びた。これはまさに指数関数的な増加だね。
最初の2日間は2-3件インスタ上にポストされていただけだった。でも、いつの間にやら、この最近は2日間で100万リポストされている!変化がどんどん急になっていくんだ。

しゅんしゅんしゅん…ぶぅわああああああ!って増えるのね?

え?ま、まあ…そんな感じ…
数学知識:対数関数(パッサパサになっていくパン)
パンは、焼き立てがおいしい。その焼き立てのおいしさは、1時間しか続かなかったりするよね。(これは対数関数説明用の適当なものです。)
それからしばらくは、だーんだんパサパサしてくる。でも、作ってから12時間を超えたくらいから、パサパサ度が増してはいるけど、その状態が結構長いこと安定している。
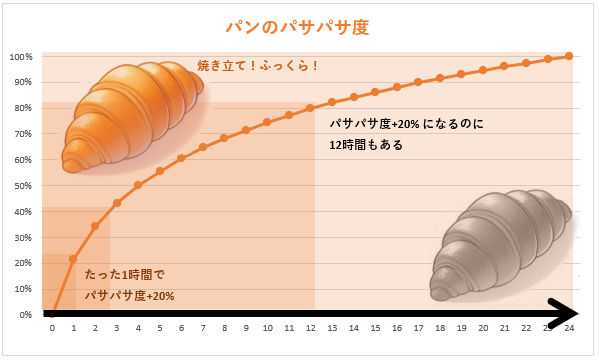
パンが店頭に並んでから時間が経過すると、老化や乾燥が進み、鮮度と美味しさが徐々に落ちていくよね。これをグラフに表すと、下記のようなグラフになる。これが対数関数的な動きだ。
100%がめっちゃパサパサしている状態なんだけど、0%から20%にいくには1時間だけど、
80%から100%にいくには12時間かかる。変化がどんどんゆっくりになっていくんだ。

ぶわあああっ…しゅんしゅんしゅんってだんだん増えなくなるのね?

ま、まあ、ちっちゃい子でもわかるように説明するならそうなる。
応用力を高める
ここの説明は第4回でやろうと思っているよ。
ここからは応用力が必要で、少し難しい話になってくる。これは文系だろうが理系だろうが、多少しっかりとした数学的な知識を積み込まないと、実践出来るようにはならないのだけど、存在を知っておけばある程度の意味は掴み取る事
従ってここでは、「そういう考え方で証拠固めしているのか!」「そういう考え方で証拠固めできるのか!」という事を掴んでもらえればまずは大丈夫。あとは、これを連想した時に、実際の仕事に合わせて調べて身につけていくと一番自分の身になりやすいと思うよ!
期待値

期待値は意思決定に不可欠な概念だよ。単に「期待値」とだけ言った場合は、リターンの得られる可能性×リターンの大きさを示すことが多い。投資や新規事業の判断においては、リスクとリターンのバランスを見極める能力が必要になる。ローリスク・ローリターン、ハイリスク・ハイリターンとか言うよね。リスクは失敗の可能性や損失の大きさを表す「マイナスの期待値」、リターンは成功の可能性や利益の大きさを表す「プラスの期待値」と考えると良いよ。
毎日1個限定発売のパン、どちらを販売すべきか?
10,000円するスペシャルチーズパンは、売れる確率が40%
5,000円するスペシャルカレーパンは、売れる確率が90%
どっちを売ったほうが売上が上がりやすい?答えはスペシャルカレーパンだ。
スペシャルチーズパン:10,000円 ✕ 40% = 4,000円(売上の期待値)
スペシャルカレーパン: 5,000円 ✕ 90% = 4,500円(売上の期待値)
標本調査と母集団

(パンを頭に乗せてはいけません)
標本調査は全数調査が難しい場合の有力な代替調査手段の1つなんだ。母集団、標本と言う言葉が重要なのでそれが何かを説明するね。
1日10,000個パンを作っているとして、全てのパンの味がおいしいかどうかを確認したいとしましょう。その時、10,000個食べたら売るものがなくなっちゃうよね。そこで、いくつかのパンを味見して、「全部問題ないだろう!」と推測を立てることができるんだ。
この時、10,000個のパンが母集団、いくつか味見することを標本調査、と言うんだ。視聴率なんかもこの考え方で算出されているよ。
仮説検定

仮説検定では、データに基づいて想像したストーリー(仮説)の真偽を判断するよ。ある水準を設け、それを超えれば仮説が正しいとみなす確認手法(検定)で、様々な研究にも応用(というかそういう人たちにとっては基礎中の基礎)されるものだよ。
いつも、1種類のパンにつき1日平均100個販売していたとして、アップルパンは1週間販売データを収集したところ、1日平均105個販売だった。これが、
この1週間だけたまたまアップルパンが売れたのか?アップルパンは本当に人気商品である可能性が高いのか?
これらを科学的に検証できる手法なんだ。今後アップルパンの販売を続けるかどうか判断するときに、たまたま1週間が好調だっただけで続けてみたら100個/日の普通の商品だった・・・となると悲しいからね。とても有効な方法なんだ。
ここまで興味を持った方ならば、こういう難しい用語を使わない動画で学ぶのもとても有効だよ。田中嘉博さんの動画は、マジでわかりやすいです。
おわりに
以上、文系でも押さえておきたい数学的基礎知識をまとめました。これらを体系的に学ぶことで思考力が向上し、仕事の幅も広がるはずです。
文系だから、低学歴だから、という理由で数学的知識に全く目を向けない人は実際多い。しかし、これは学校の勉強で全てを理解しないと点数が取れない形になっていることや、その結果、点数が低いことに対してゼロイチ判定で私は俺は向いてないって思ってしまっているところに原因があると思う。
実際、社会人になったときこそ、データ活用のチャンスが多く訪れるので、この機会に自分自身の実例と並べて数学的知識をきちんと身につけてみよう。
ゼロイチ判定から抜け出して欲しい記事はこちら。

30代半ばのサラリーマンです!入社早々から4-5年は、周囲の上司や先輩に酷く追い詰められた経験あり。早朝深夜残業サービス当たり前。今ではそんなしょうもない類の人達を努力で出し抜いて成績優秀者として報奨を得たり役職者になる事ができました。自由に、楽しく、家族第一、それでも活躍できるサラリーマンを日々目指しています。苦しみ悩む社会人を応援するためにブログ発信を決意。



コメント